Which Principal Energy Level Change By The Electron

Unlike states of quantum systems

Energy levels for an electron in an cantlet: ground land and excited states. Afterward absorbing energy, an electron may "jump" from the ground country to a higher energy excited land.

A quantum mechanical system or particle that is jump—that is, confined spatially—can simply accept on sure discrete values of energy, called energy levels. This contrasts with classical particles, which can have any amount of energy. The term is commonly used for the free energy levels of the electrons in atoms, ions, or molecules, which are bound by the electric field of the nucleus, only can likewise refer to free energy levels of nuclei or vibrational or rotational energy levels in molecules. The energy spectrum of a system with such discrete energy levels is said to be quantized.

In chemistry and diminutive physics, an electron crush, or chief free energy level, may be thought of as the orbit of ane or more electrons around an atom'due south nucleus. The closest shell to the nucleus is called the "1 beat out" (too called "M shell"), followed past the "2 shell" (or "L shell"), so the "3 shell" (or "M shell"), and so on further and farther from the nucleus. The shells correspond with the principal quantum numbers (due north = 1, two, 3, iv ...) or are labeled alphabetically with letters used in the X-ray notation (K, L, Grand, N...).

Each shell tin can incorporate simply a stock-still number of electrons: The first shell can agree up to ii electrons, the second shell can hold up to viii (ii + 6) electrons, the third shell can concord up to eighteen (2 + half dozen + 10) and and then on. The general formula is that the due northth crush can in principle concord up to 2n ^two electrons.^[ane] Since electrons are electrically attracted to the nucleus, an cantlet's electrons will generally occupy outer shells merely if the more than inner shells have already been completely filled past other electrons. However, this is non a strict requirement: atoms may have 2 or even iii incomplete outer shells. (See Madelung dominion for more details.) For an caption of why electrons be in these shells see electron configuration.^[two]

If the potential energy is set to zero at infinite distance from the atomic nucleus or molecule, the usual convention, then bound electron states have negative potential energy.

If an cantlet, ion, or molecule is at the lowest possible energy level, it and its electrons are said to be in the ground state. If it is at a higher free energy level, information technology is said to be excited, or any electrons that take higher free energy than the ground state are excited. If more than ane breakthrough mechanical country is at the aforementioned energy, the energy levels are "degenerate". They are then called degenerate free energy levels.

Caption [edit]

Wavefunctions of a hydrogen atom, showing the probability of finding the electron in the space around the nucleus. Each stationary state defines a specific free energy level of the atom.

Quantized energy levels upshot from the wave behavior of particles, which gives a relationship between a particle'south energy and its wavelength. For a confined particle such as an electron in an cantlet, the wave functions that accept well divers energies take the class of a continuing wave.^[iii] States having well-defined energies are called stationary states because they are us that do not change in time. Informally, these states correspond to a whole number of wavelengths of the wavefunction along a closed path (a path that ends where it started), such every bit a round orbit around an atom, where the number of wavelengths gives the type of atomic orbital (0 for s-orbitals, 1 for p-orbitals and so on). Elementary examples that show mathematically how energy levels come about are the particle in a box and the breakthrough harmonic oscillator.

Any superposition (linear combination) of energy states is also a breakthrough land, merely such states change with time and do not have well-defined energies. A measurement of the energy results in the collapse of the wavefunction, which results in a new state that consists of just a single energy state. Measurement of the possible energy levels of an object is called spectroscopy.

History [edit]

The first evidence of quantization in atoms was the observation of spectral lines in calorie-free from the sun in the early 1800s by Joseph von Fraunhofer and William Hyde Wollaston. The notion of energy levels was proposed in 1913 by Danish physicist Niels Bohr in the Bohr theory of the atom. The modern quantum mechanical theory giving an caption of these energy levels in terms of the Schrödinger equation was avant-garde by Erwin Schrödinger and Werner Heisenberg in 1926.

Atoms [edit]

Intrinsic energy levels [edit]

In the formulas for energy of electrons at various levels given below in an atom, the nil indicate for energy is set when the electron in question has completely left the atom, i.e. when the electron'south primary breakthrough number $northward = \infty$ . When the electron is leap to the cantlet in any closer value of $n$ , the electron'southward energy is lower and is considered negative.

Orbital state energy level: atom/ion with nucleus + 1 electron [edit]

Assume there is i electron in a given atomic orbital in a hydrogen-like cantlet (ion). The energy of its state is mainly adamant past the electrostatic interaction of the (negative) electron with the (positive) nucleus. The energy levels of an electron around a nucleus are given by :

E_{n}=-hcR_{\infty }{\frac {Z^{two}}{n^{2}}}

(typically between ane eV and 10³ eV), where $R \infty$ is the Rydberg constant, $Z$ is the atomic number, $n$ is the principal quantum number, $h$ is Planck'due south abiding, and $c$ is the speed of light. For hydrogen-like atoms (ions) only, the Rydberg levels depend only on the master quantum number $n$ .

This equation is obtained from combining the Rydberg formula for whatsoever hydrogen-like element (shown below) with $Due east = h ν = h c / λ$ assuming that the principal quantum number $n$ above = $n 1$ in the Rydberg formula and $n 2 = \infty$ (principal quantum number of the energy level the electron descends from, when emitting a photon). The Rydberg formula was derived from empirical spectroscopic emission data.

{\frac {one}{\lambda }}=RZ^{2}\left({\frac {i}{n_{i}^{ii}}}-{\frac {i}{n_{2}^{2}}}\right)

An equivalent formula can exist derived breakthrough mechanically from the time-independent Schrödinger equation with a kinetic free energy Hamiltonian operator using a moving ridge office as an eigenfunction to obtain the energy levels as eigenvalues, simply the Rydberg constant would be replaced by other cardinal physics constants.

Electron-electron interactions in atoms [edit]

If in that location is more than than i electron effectually the atom, electron-electron-interactions enhance the energy level. These interactions are often neglected if the spatial overlap of the electron wavefunctions is low.

For multi-electron atoms, interactions between electrons cause the preceding equation to be no longer accurate every bit stated just with $Z$ equally the atomic number. A unproblematic (though not consummate) manner to sympathise this is as a shielding effect, where the outer electrons see an effective nucleus of reduced accuse, since the inner electrons are bound tightly to the nucleus and partially cancel its charge. This leads to an approximate correction where $Z$ is substituted with an constructive nuclear charge symbolized every bit $Z eff$ that depends strongly on the principal quantum number.

E_{northward,\ell }=-hcR_{\infty }{\frac {{Z_{\rm {eff}}}^{2}}{due north^{ii}}}

In such cases, the orbital types (determined past the azimuthal quantum number $ℓ$ ) as well equally their levels within the molecule affect $Z eff$ and therefore also affect the various atomic electron energy levels. The Aufbau principle of filling an cantlet with electrons for an electron configuration takes these differing energy levels into account. For filling an atom with electrons in the footing country, the lowest energy levels are filled first and consistent with the Pauli exclusion principle, the Aufbau principle, and Hund'due south rule.

Fine construction splitting [edit]

Fine structure arises from relativistic kinetic energy corrections, spin–orbit coupling (an electrodynamic interaction between the electron'due south spin and motion and the nucleus'south electric field) and the Darwin term (contact term interaction of s shell^{[ which? ]} electrons within the nucleus). These affect the levels by a typical order of magnitude of 10⁻³ eV.

Hyperfine structure [edit]

This even effectively structure is due to electron–nucleus spin–spin interaction, resulting in a typical alter in the energy levels by a typical club of magnitude of 10⁻⁴ eV.

Free energy levels due to external fields [edit]

Zeeman upshot [edit]

There is an interaction free energy associated with the magnetic dipole moment, $μ L$ , arising from the electronic orbital angular momentum, $L$ , given by

U=-{\boldsymbol {\mu }}_{L}\cdot \mathbf {B}

with

-{\boldsymbol {\mu }}_{Fifty}={\dfrac {e\hbar }{2m}}\mathbf {L} =\mu _{B}\mathbf {L}

Additionally taking into account the magnetic momentum arising from the electron spin.

Due to relativistic effects (Dirac equation), there is a magnetic momentum, $μ Due south$ , arising from the electron spin

-{\boldsymbol {\mu }}_{Due south}=-\mu _{B}g_{Due south}\mathbf {S}

with $grand Due south$ the electron-spin g-factor (near 2), resulting in a full magnetic moment, $μ$ ,

{\boldsymbol {\mu }}={\boldsymbol {\mu }}_{L}+{\boldsymbol {\mu }}_{South}

The interaction energy therefore becomes

U_{B}=-{\boldsymbol {\mu }}\cdot \mathbf {B} =\mu _{B}B(M_{L}+g_{Due south}M_{S})

Stark effect [edit]

Molecules [edit]

Chemical bonds between atoms in a molecule form because they brand the situation more stable for the involved atoms, which generally ways the sum free energy level for the involved atoms in the molecule is lower than if the atoms were non so bonded. As separate atoms approach each other to covalently bail, their orbitals bear on each other's free energy levels to form bonding and antibonding molecular orbitals. The energy level of the bonding orbitals is lower, and the energy level of the antibonding orbitals is higher. For the bond in the molecule to be stable, the covalent bonding electrons occupy the lower free energy bonding orbital, which may be signified by such symbols as σ or π depending on the state of affairs. Respective anti-bonding orbitals can be signified past adding an asterisk to go σ* or π* orbitals. A non-bonding orbital in a molecule is an orbital with electrons in outer shells which do not participate in bonding and its energy level is the aforementioned as that of the elective atom. Such orbitals can be designated as n orbitals. The electrons in an north orbital are typically alone pairs. ^[4] In polyatomic molecules, different vibrational and rotational energy levels are likewise involved.

Roughly speaking, a molecular free energy land, i.due east. an eigenstate of the molecular Hamiltonian, is the sum of the electronic, vibrational, rotational, nuclear, and translational components, such that:

E=E_{\text{electronic}}+E_{\text{vibrational}}+E_{\text{rotational}}+E_{\text{nuclear}}+E_{\text{translational}}

where $E electronic$ is an eigenvalue of the electronic molecular Hamiltonian (the value of the potential energy surface) at the equilibrium geometry of the molecule.

The molecular free energy levels are labelled past the molecular term symbols. The specific energies of these components vary with the specific energy country and the substance.

Energy level diagrams [edit]

There are various types of energy level diagrams for bonds betwixt atoms in a molecule.

Examples: Molecular orbital diagrams, Jablonski diagrams, and Franck–Condon diagrams.

Energy level transitions [edit]

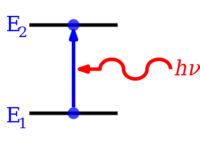
An increase in energy level from $E ane$ to $Due east 2$ resulting from absorption of a photon represented by the red squiggly arrow, and whose energy is $h ν$

A decrease in energy level from $Eastward two$ to $E 1$ resulting in emission of a photon represented by the blood-red squiggly arrow, and whose energy is $h ν$

Electrons in atoms and molecules can modify (make transitions in) energy levels by emitting or absorbing a photon (of electromagnetic radiation), whose energy must be exactly equal to the energy difference between the ii levels. Electrons can too be completely removed from a chemical species such as an atom, molecule, or ion. Complete removal of an electron from an atom tin can be a class of ionization, which is effectively moving the electron out to an orbital with an infinite principal breakthrough number, in issue and then far away then as to have practically no more effect on the remaining atom (ion). For various types of atoms, there are 1st, 2d, 3rd, etc. ionization energies for removing the 1st, and so the second, then the tertiary, etc. of the highest energy electrons, respectively, from the atom originally in the basis state. Energy in corresponding opposite quantities tin can too be released, sometimes in the form of photon energy, when electrons are added to positively charged ions or sometimes atoms. Molecules can also undergo transitions in their vibrational or rotational energy levels. Free energy level transitions tin can also exist nonradiative, significant emission or absorption of a photon is not involved.

If an cantlet, ion, or molecule is at the lowest possible energy level, it and its electrons are said to be in the ground country. If information technology is at a higher free energy level, it is said to be excited, or whatsoever electrons that take higher energy than the basis state are excited. Such a species can be excited to a higher energy level by arresting a photon whose energy is equal to the energy difference between the levels. Conversely, an excited species tin can become to a lower energy level by spontaneously emitting a photon equal to the energy deviation. A photon'due south free energy is equal to Planck'south constant ( $h$ ) times its frequency ( $f$ ) and thus is proportional to its frequency, or inversely to its wavelength ( $λ$ ).^[4]

Δ Eastward = h f = h c / λ

since $c$ , the speed of light, equals to $f λ$ ^[four]

Correspondingly, many kinds of spectroscopy are based on detecting the frequency or wavelength of the emitted or absorbed photons to provide information on the material analyzed, including information on the energy levels and electronic structure of materials obtained by analyzing the spectrum.

An asterisk is commonly used to designate an excited land. An electron transition in a molecule's bond from a footing state to an excited state may have a designation such as σ → σ*, π → π*, or n → π* pregnant excitation of an electron from a σ bonding to a σ antibonding orbital, from a π bonding to a π antibonding orbital, or from an due north non-bonding to a π antibonding orbital. ^[iv] ^[5] Opposite electron transitions for all these types of excited molecules are also possible to return to their footing states, which can be designated as σ* → σ, π* → π, or π* → n.

A transition in an energy level of an electron in a molecule may be combined with a vibrational transition and called a vibronic transition. A vibrational and rotational transition may be combined by rovibrational coupling. In rovibronic coupling, electron transitions are simultaneously combined with both vibrational and rotational transitions. Photons involved in transitions may have energy of diverse ranges in the electromagnetic spectrum, such as 10-ray, ultraviolet, visible calorie-free, infrared, or microwave radiation, depending on the type of transition. In a very general way, energy level differences between electronic states are larger, differences between vibrational levels are intermediate, and differences between rotational levels are smaller, although there can be overlap. Translational energy levels are practically continuous and can be calculated equally kinetic energy using classical mechanics.

Higher temperature causes fluid atoms and molecules to move faster increasing their translational energy, and thermally excites molecules to higher average amplitudes of vibrational and rotational modes (excites the molecules to college internal energy levels). This means that every bit temperature rises, translational, vibrational, and rotational contributions to molecular heat capacity permit molecules absorb rut and hold more than internal free energy. Conduction of heat typically occurs as molecules or atoms collide transferring the heat between each other. At even higher temperatures, electrons can be thermally excited to higher energy orbitals in atoms or molecules. A subsequent drop of an electron to a lower energy level can release a photon, causing a perchance colored glow.

An electron farther from the nucleus has college potential energy than an electron closer to the nucleus, thus it becomes less bound to the nucleus, since its potential free energy is negative and inversely dependent on its distance from the nucleus.^[6]

Crystalline materials [edit]

Crystalline solids are plant to have free energy bands, instead of or in addition to energy levels. Electrons tin can have on any energy inside an unfilled band. At starting time this appears to be an exception to the requirement for energy levels. Yet, as shown in band theory, energy bands are actually fabricated up of many detached energy levels which are as well close together to resolve. Within a band the number of levels is of the order of the number of atoms in the crystal, then although electrons are actually restricted to these energies, they appear to be able to take on a continuum of values. The of import free energy levels in a crystal are the top of the valence band, the lesser of the conduction band, the Fermi level, the vacuum level, and the energy levels of whatsoever defect states in the crystal.

See likewise [edit]

Perturbation theory (breakthrough mechanics)
Computational chemistry

References [edit]

^ Re: Why exercise electron shells have gear up limits ? madsci.org, 17 March 1999, Dan Berger, Faculty Chemistry/Science, Bluffton College
^ Electron Subshells. Corrosion Source. Retrieved on 1 December 2011.
^ Tipler, Paul A.; Mosca, Gene (2004). Physics for Scientists and Engineers, 5th Ed. Vol. two. Westward. H. Freeman and Co. p. 1129. ISBN0716708108.
^ ^a ^b ^c ^d UV-Visible Absorption Spectra
^ Theory of Ultraviolet-Visible (UV-Vis) Spectroscopy
^ "Archived copy". Archived from the original on 2010-07-xviii. Retrieved 2010-ten-07 . {{cite spider web}}: CS1 maint: archived copy equally title (link)